11.4.2.2.2 : Loi d'Amdahl
La loi d'Amdahl donne l'accélération théorique $\alpha$ d'un programme dont l'exécution se compose de phases d'exécution séquentielles et de phases d'exécution parfaitement parallèles, en fonction de la fraction $p$ de son code qui peut être parallélisée et du nombre de cœurs $n$ sur lequel cette fraction est exécutée dans la version parallèle.
$$\begin{eqnarray*} \alpha & = & \dfrac{1}{1 - p + \frac{p}{n}} \end{eqnarray*}$$
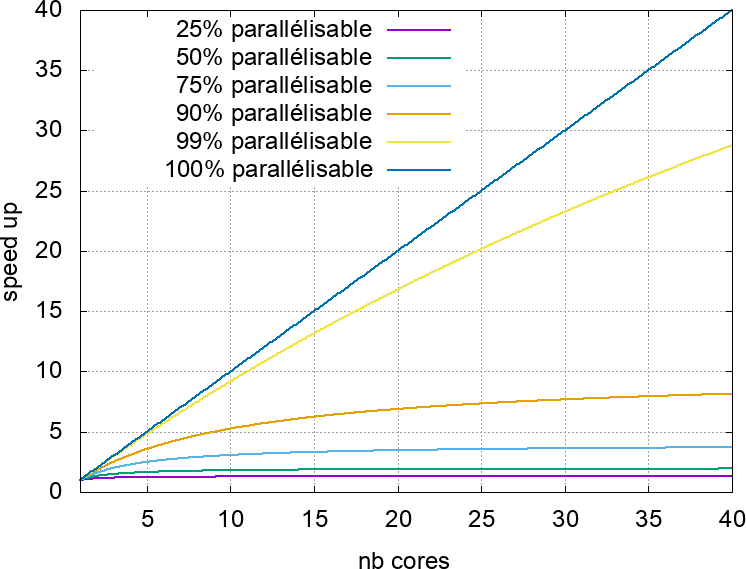
La figure 43 montre différents exemples d'accélérations que l'on peut attendre suivant le niveau de parallélisation du programme utilisé.
Figure 43 : Illustration de la loi d'Amdahl.
On voit que plus le nombre de cœurs $n$ d'un système parallèle est important, plus il est difficile d'accélérer un traitement donné d'un facteur même approximativement égal à $n$ en l'exécutant en parallèle sur ce système.