11.6.2.2 : La programmation
Un bon nombre d'exemples du livre [174]OpenCL in Action, 2012, Matthew Scarpino ont été adaptés (si nécessaire), compilés et exécutés sur la carte DE1-SoC mais surtout sur la Cyclone V GT, toujours avec la réserve que certaines fonctionnalités OpenCL n'étaient pas disponibles pour les FPGA à l'étude, au moins avec les BSP utilisés. L'exemple le plus complexe qui a été le mieux analysé est la Transformée Fourier Discrète (TFD), dans sa version rapide (TFDR, à ne pas confondre avec la transformée rapide FFT, Fast Fourier Transformation).
La Transformée de Fourier Discrète d'un signal échantillonné est donné par la formule~:
$$\begin{eqnarray*} X_{k} & = & \sum_{n=0}^{N-1} x_{n} e^{-i2\pi kn/N} ~~~~~~,~~~ k = 0 \dots (N - 1) \end{eqnarray*}$$
où on peut considérer pour la simplicité que $x_{n}$ sont des nombres réels. La transformée est exprimée par les nombres complexes $X_{k}$ , avec une partie réelle et une partie imaginaire. Les valeurs en module $|X_{k}|$ donnent les composantes de la puissance spectrale. Les valeurs $x_{n}$ seront générées de façon aléatoire dans un intervalle fixe. La longueur $N$ est variée, mais gardée toujours à une puissance entière de 2 et pour chaque longueur un grand nombre d'échantillons est généré, pour avoir une statistique sur le temps d'exécution.
La solution directe et sans aucune optimisation est celle-ci~:
for (k = 0 ; k < N ; ++k)
Xre[k] = 0;
Xim[k] = 0;
for (n = 0 ; n < N ; ++n)
Xre[k] += x[n] * cos(n * k * PI2 / N);
Xim[k] -= x[n] * sin(n * k * PI2 / N);
Dans ce code on effectue $N^{2}$ calculs de composante. La version rapide de la transformée est basée sur le fait qu'on peut exprimer la transformée comme une somme de deux termes~:
$$\begin{eqnarray*} X_{k} = E_{k} + e^{-\frac{2\pi i}{N} k} O_{k} ~~~,~~~ X_{k+\frac{N}{2}} = E_{k} - e^{-\frac{2\pi i}{N} k} O_{k}~~~~~~,~~~ k = 0 \dots (\frac{N}{2} - 1) \end{eqnarray*}$$
avec $E_{k}$ et $O_{k}$ les transformées de la partie du signal $x_{n}$ formée par les index pairs et les index impairs, respectivement. Le procédé de partition paire - impaire continue jusqu'à la longueur triviale du vecteur de valeurs. Le code pour la variante CPU qui accompagne le livre [174]OpenCL in Action, 2012, Matthew Scarpino se trouve ici [167]Code pour la Transformée Fourier Discrète.
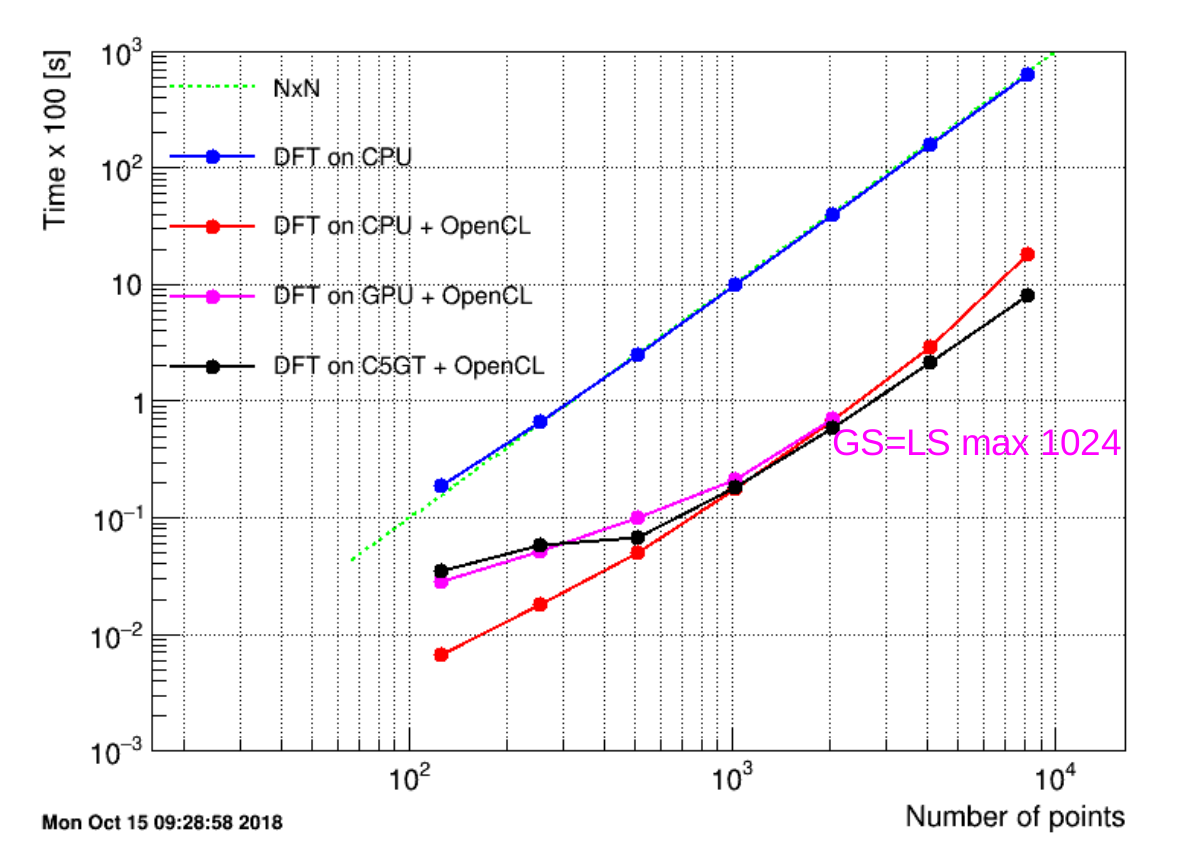
Les résultats présentés dans la figure 50 ont été obtenus avec la dimension $N$ variée de 128 ($2^{7}$ ) à 8192 ($2^{13}$ ). Pour chaque dimension $N$ , le temps d'exécution a été moyenné sur 100 itérations, avec l'image FPGA binaire chargée une seule fois au début. Plus le temps est long, moins le calcul est efficace en rapidité d'exécution. La courbe bleue, linéaire en échelle double logarithmique, représente la dépendance $N^{2}$ de l'algorithme direct de calcul de la TFD. Sur le même graphique on peut voir les résultats obtenus avec la variante TFDR parallélisé avec OpenCL sur trois périphériques de calcul~: CPU (Intel Xeon E5-1607, 3GHz), GPU (NVidia Quadro 2000M, 1.1GHz) et FPGA (Cyclone V GT). Grâce à l'astuce de calcul rapide de la TFD, le nombre de items qui s'exécutent en parallèle est la moitié de la longueur $N$ du vecteur à transformer. Les résultats avec le GPU s'arrêtent à $N = 2048$ , limités par la capacité de cette carte graphique (maximum number of threads per block $= 1024$ ).
Figure 50 : La Transformée Fourier Discrète Rapide parallélisée avec OpenCL sur CPU, GPU et FPGA
On peut voir dans le graphique que dans cet exemple relativement simple (sans branchement dans l'exécution des instructions à l'intérieur du noyau, juste des boucles for) le FPGA peut être parfois un peu plus efficace que le CPU avec OpenCL et qu'il peut concurrencer un vieux type de GPU. Son avantage par rapport au GPU consiste dans le fait qu'il peut passer à l'échelle le nombre d'items d'exécution pour des valeurs plus grandes que $N$ .
Outre l'observation du temps total d'exécution, une étude plus détaillée a été menée pour séparer, par exemple, le temps de transfert des données à transformer vers la mémoire interne du FPGA. Ceci peut évidemment pénaliser la performance globale et il dépend essentiellement de la gamme du matériel utilisé, par exemple la vitesse de la connexion PCIe.
OpenCL utilise aussi un autre type d'accélération, basé sur la vectorisation des opérandes et des opérations élémentaires appliquées dessus. Les types de vecteurs sont dérivés des types de scalaires (pas toutes) et donnent~: char$n$ , uchar$n$ , $\dots$ , float$n$ , avec valeurs possibles $n = 2, 3, 4, 8$ et $16$ (la largeur de vecteur préférée est indiquée par l'implémentation particulière dans le device ciblé). Le cas de la double précision dépend essentiellement du device utilisé, pour les FPGA en étude il n'est pas possible de faire des calculs en double précision.
Une opération avec vecteurs s'écrit en OpenCL~:
float4 data_vec_1 = (float4) (1.4, 2.3, 3.2, 4.1);
float4 data_vec_2 = (float4) (0.1, 0.2, 0.3, 0.4);
float4 data_vec_3 = data_vec_1 + data_vec_2;
et les composantes du vecteur résultant en float scalaire seront accessibles par~:
data_vec_3.s0, data_vec_3.s1, data_vec_3.s2, data_vec_3.s3