11.8.1 : Introduction
La précision, et sa banalisation ("commoditization") notamment en raison de l'effondrement de son coût, et particulièrement de sa reproductibilité, est à l'origine de nos sociétés industrielles depuis le milieu du XVIII\ieme siècle. L'évolution de la précision numérique est allée encore plus vite et encore plus loin que la précision mécanique.
Figure 57 : Norme IEEE 754 qui décrit les flottants 32 et 64 bits mais aussi 80 et 16 bits.
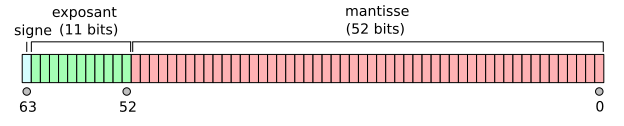
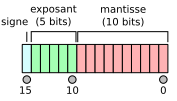
Après un développement assez anarchique des formats et des algorithmes de calcul en virgule flottante à l'origine du secteur informatique, une norme a émergé en~1985 qui a standardisé les formats : IEEE 754~[191]On a Proposed Floating-point Standard, 1979, Kahan, William and Palmer, John F.[197]IEEE Standard for Binary Floating-Point Arithmetic, 1985[200]IEEE Standard for Radix-Independent Floating-Point Arithmetic, 1987 (voir figure 57) et ses évolutions~[198]IEEE Standard for Floating-Point Arithmetic, 2008[199]IEEE Standard for Floating-Point Arithmetic, 2019.
Outre un standard de format, cette norme fournit des garanties de précision pour les diverses opérations et fonctions, ainsi qu'une interface avec la FPU (Floating Point Unit) sous forme de contrôle du mode d'arrondi, de flag de statut, de représentation des nombres exceptionnels ou dénormaux et d'exceptions masquables en cas de débordement, de division par zéro, d'indétermination voire de calcul inexact. Les puristes reprochent l'impact de cette approche sur les performances (exception et dénormaux) et sur l'efficacité de la représentation.
Ses défauts ne doivent pas nous faire oublier ses nombreuses avancées et la situation antérieure. Le parti pris de cette norme a été de donner une forme de contrôle à l'utilisateur sur cette boite noire qu'est le calcul numérique, et des moyens pour surveiller la précision tout en gardant la performance. Avant même cette standardisation, il faut porter au crédit du langage C d'avoir permis une amélioration de la garantie des résultats numériques en procédant à tous les calculs intermédiaires en double précision, dans sa version Kernighan and Ritchie, avant sa normalisation ANSI C toutefois.
Les apports de cette norme sont toutefois restés cantonnés à une petite communauté~: bien que la large implantation d'Intel, promoteur de cette norme, ait amené ces fonctionnalités sur tous les bureaux depuis le coprocesseur~8087, rares ont été les systèmes et les langages à proposer la double précision étendue (64 bits de mantisse) ou les flottants en base dix (pourtant cruciaux pour les calculs comptables), sans parler de propager l'interface du FPU dans les bibliothèques de ces langages...
Mais avant même de faire des erreurs dans les calculs, le simple recours à la base dix sur du matériel qui travaille en base deux introduit une erreur.