6.2.1 : Algorithme force brute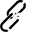



L'algorithme force brute consiste à calculer toutes les interactions entre toutes les particules. La seule optimiation que l'on s'autorisera sera de calculer chaque force qu'une seule fois, car entre deux particules $1$ et $2$ la force de $1$ sur $2$ est la même que celle de $2$ sur $1$ .

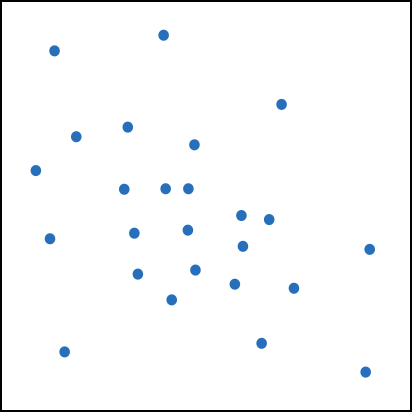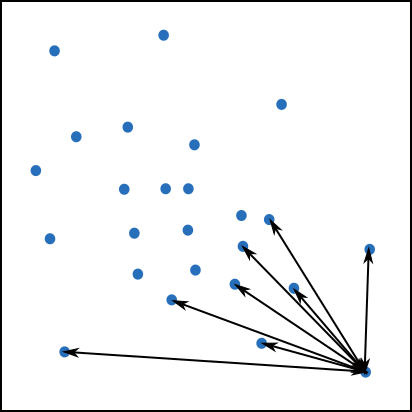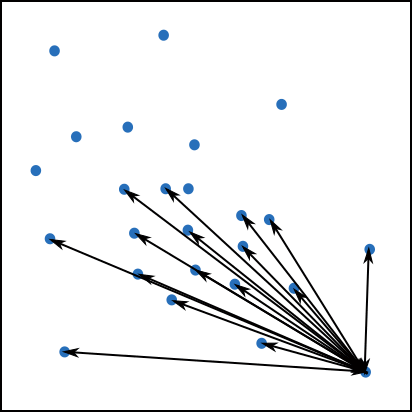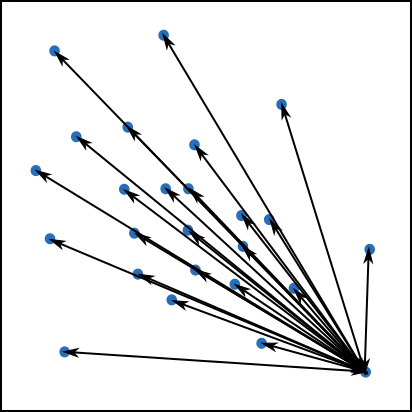
La figure 14 illustre le calcul des interactions entre une particules et toutes les autres à deux dimensions.

nothing

Figure 14 : Illustration du calcul des interactions entre une particule et toutes les autres.

La complexité de cet algorithme est donc de $2$ parmis $N$ soit : $$\begin{eqnarray*} C^k_n & = & \dfrac{n!}{k!(n-k)!} \quad \text{avec } k = 2 \end{eqnarray*}$$ Soit : $$\begin{eqnarray*} C^2_n & = & \dfrac{n!}{2(n-2)!} \\ & = & \dfrac{n(n-1)}{2} \end{eqnarray*}$$ Où $n$ est le nombre d'interactions à calculer, soit $n = N - 1$ . On ne calcule pas l'interaction d'une particule avec elle-même.

Ce qui donne $24\times 23 /2 = 276$ calculs d'interaction.

Cette complexité varie donc en $O\left(N^2\right)$ ce qui posera un problème pour un grand nombre de particules.