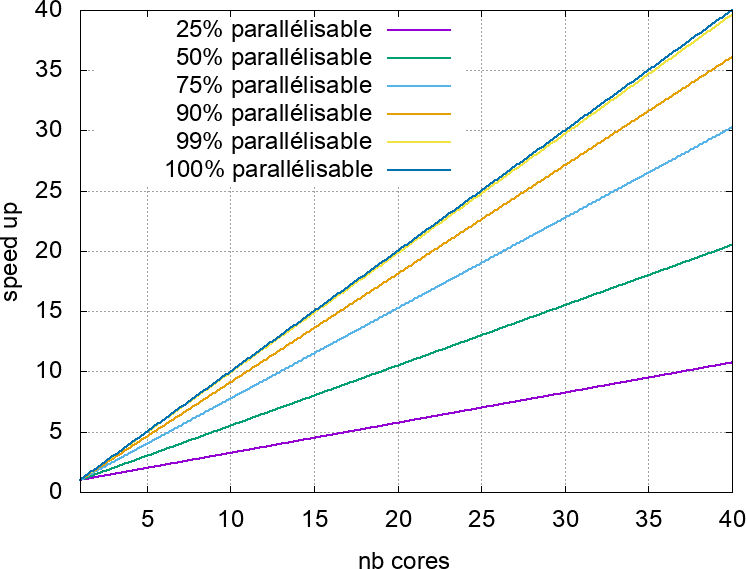
11.4.2.2.3 : Loi de Gustafson
La loi d'Amdhal montre qu'on ne peut pas accélérer indéfiniment la résolution d'un problème donné en augmentant le niveau de parallélisme. Ce faisant, elle fixe des limites au degré auquel l'utilisation du parallélisme peut être utilisé pour optimiser un calcul existant.
Mais par construction, elle ne prend pas en compte le fait que l'augmentation des ressources des centres de calcul n'est généralement pas motivée par l'accélération des calculs existants, mais plutôt par la volonté de résoudre de nouveaux problèmes de plus grande taille sans que le temps de calcul ne devienne déraisonnable.
Dans ces circonstances, il peut être aussi pertinent d'étudier ce qui se passe pour un calcul qui n'est plus de taille fixe, mais dont la taille du cœur de calcul parallélisable augmente avec le nombre $n$ de cœurs disponibles. On a alors une accélération par rapport au même calcul effectué sur un processeur séquentiel qui est donnée par la loi de Gustafson~:
$$\begin{eqnarray*} \alpha & = & n + (1 - n) \times s \end{eqnarray*}$$
Où $s$ est la fraction du calcul qui est séquentielle à $n = 1$ .
L'étude de cette loi (voir figure 44) montre que, sous certaines hypothèses, l'augmentation du parallélisme est toujours pertinente quand elle est motivée par la résolution de problèmes plus complexes. La réduction de la portion séquentielle du programme n'a alors pour objectif que d'utiliser plus efficacement les ressources de calcul ajoutées.
Figure 44 : Illustration de la loi de Gustafson.